By Sertalp B. Cay | January 8, 2021
The amount of available content for Fantasy Premier League (FPL) is unbelivable and hard to follow. Among all, one of my favorite resources is the “Corridor of Uncertainty” podcast as they focus on modeling and analytics part of FPL. Their guest in the latest episode was Abdul Rehman (FPL Salah), who is a well-known manager in the FPL community. I truly enjoyed their discussion and noticed that the word “optimal” is thrown around quite a bit. Since I do optimization for a living, it makes me happy to hear it in everyday conversations, especially regarding FPL.
FPL is the picture-perfect example for demonstrating how optimization could be useful. Why? Because (mathematical) optimization deals with making the best out of limited resources under restrictions. Fantasy sports –with their well-defined rules, and standard ways of measuring the performance– are great showcases.
As I have mentioned before, so-called “Effective Ownership” (EO) is a controversial topic among FPL managers.
This is where Effective Ownership comes into play. If you’re playing for a personal points tally it’s all good, if you’re playing for points relative to other managers eg rank,then EO and differentials come into play. That’s why EO is a “thing”.
— FFScout_Mark (@FFScout_Mark) December 23, 2020
This is something I’m incredibly passionate about.
— Az (@fplblackbox_az) December 23, 2020
There is no “advantage / disadvantage” that can be made on the TC when you base it on others.
If you TC the player who gets the most points, you’ve done the best you can. It doesn’t matter what everyone else is doing!!!
Yes, AZ is right, optimal decision is independent of EO, but we need to take a step back to understand why.
The role ‘ownership’ plays in optimal solution
There are two schools of thought:
- The first group says that if you try to maximize your points, you will be doing the best you could regardless of what others are doing. Period.
- The second group claims that the Effective Ownership makes it useless to own highly-owned players (unless you captain them), so EO does matter.
As far as I can tell, the confusion comes from the missing part of the equation when we think of EO. I made the same mistake in my earlier blog post, so I will talk a little bit more about EO here.
Suppose Salah will get 8 points next game and he is owned by 40% of all FPL managers including you. To keep things simple, let me leave out the captaincy points. You and 40% of all FPL managers will get 8 points. 60% will get 0 out of him. The average benefit you get is the difference between your gain and your loss. There is no loss to you in this case, but 40% of players will get the same benefit as you do, which will reduce your relative gain. The average that Salah will bring to FPL managers is (overall average):
$$ 8 \cdot \frac{40}{100} - 0 \cdot \frac{60}{100} = 3.2 $$
When you take your 8 points, the net gain (relative to all FPL managers) you get from Salah is 8-3.2=4.8. Awesome. For people who don’t own him, there is no gain but only loss, which is simply -3.2.
We can write down this idea in the following mathematical equation.
$$ \text{Average gain} - \text{Average loss} = $$
$$ p_i \cdot (1-o_i) \cdot x_i - p_i \cdot o_i \cdot (1-x_i) $$
Here, $x$ is a binary value, which takes value 1 if you own the player, and takes value 0 otherwise. $p$ is the (expected) points for the player, and $o$ is the ownership ratio of the player. In our earlier example, $p$ was 8, $o$ was 0.4, and for you $x$ was equal to 1. Which gives us the same result:
- If you own: $8 \cdot (1-0.4) \cdot 1 - 8 \cdot 0.4 \cdot 0= 4.8$
- If you don’t: $8 \cdot (1-0.4) \cdot 0 - 8 \cdot 0.4 \cdot 1 = -3.2$
The equation above reduces to $$ p_i x_i - p_i o_i $$
This is very intuitive: The first part $p_i \cdot x_i$ becomes 0 if you don’t own the player, and it becomes $p_i$ if you do. So, the first term is your absolute gain. The second part is simply the average points of all FPL managers getting from this particular player. The good news? The second part is constant: you cannot do anything about it, so you don’t need to care at all! If other managers own Fernandes heavily, the average will be the same regardless of what you do. The only thing you can control here is the value $x$, whether you have the player or not.
This is why EO is not important. It only changes your relative position to other FPL managers.
Maximizing your relative difference to average of all FPL managers is the same thing as maximizing your own points!
In the context of optimization, second term does not have any effect. But, the question you are probably wondering if there is a catch. There is. Enter multiobjective optimization.
Multiobjective optimization with FPL
When I defined average gain and loss, we had ownership rate appearing in both terms. So, you might be suspecting that EO changes your gain and loss, which is totally correct. Like all FPL managers we are trying to
- Maximize the gain
- Minimize the loss
These two may sound like parallel to each other, but they are actually conflicting objectives. Mainly because you have limited budget and need to decide on one player or the other. Let me explain it on an example below.
Suppose Mane and Fernandes both has the same expected points, 10, but Mane’s ownership ratio is 5% and Fernandes’ is 90%. The average gain you get from Mane (suppose they both get 10 points exactly) is $10 \cdot (1-0.05) = 9.5$. However you will lose $10 \cdot 0.9 = 9$ by not owning Fernandes. Similarly, the gain you get from Fernandes if you own him is $10 \cdot (1-0.9) = 1$, while the loss from not owning Mane is $10 \cdot 0.05 = 0.5$.
The math says that the net benefit you get by owning either of them is the same!
- Owning Mane: Gain - Loss = 9.5 - 9 = 0.5
- Owning Fernandes: Gain - Loss = 1 - 0.5 = 0.5
However, as you see there is a difference on how we reached 0.5. The first path is high risk, high reward.
- If you have Mane, and Fernandes blanks (2 points): you will jump in rank massively: $9.5 - 2 \cdot 0.9 = 7.7$.
- If you have Mane, and he blanks: you will lose quite a bit of rank: $2 \cdot (1-0.05) - 9 = -7.1$.
- If you have Fernandes, and Mane blanks: your net benefit is $1 - 2 \cdot 0.05 = 0.9$.
- If you have Fernandes, and he blanks: your net benefit is $2 \cdot (1-0.9) - 0.5 = -0.3$.
See the payoff table below.
| Scenario | Own Mane | Own Fernandes |
|---|---|---|
| Both get 10 | 0.5 | 0.5 |
| Fernandes blanks | 7.7 | -0.3 |
| Mane blanks | -7.1 | 0.9 |
| Both blanks | 0.1 | 0.1 |
It is easy to see why owning Mane could make or break things for you now.
The problem gets more complicated when you include all the players, not only 2. There are number of ways to solve multiobjective optimization problems like this one, but I will use weighted-sum method.
On my FPL Optimized page, I show the following expected gain / loss graph depending on the ownership rates:
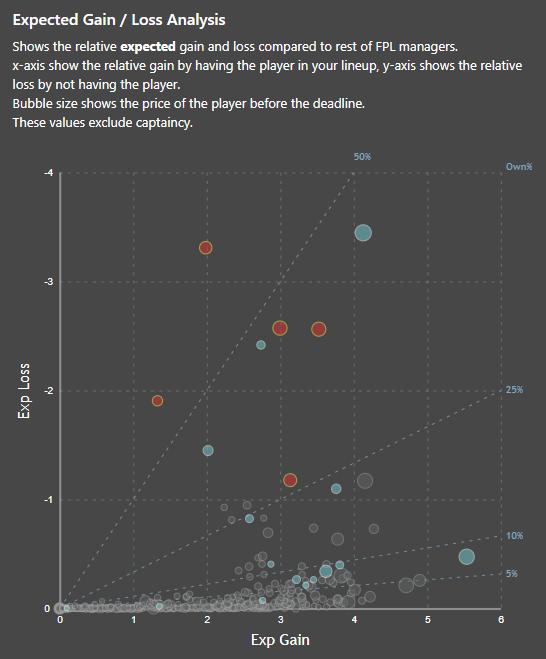
When you try to only “maximize the gain”, the optimization will pick the players higher on the x-axis. This will mean that you prefer players with “high expected points and low ownership”.
When you “minimize the loss”, the optimization will pick the players higher on the y-axis. This will mean that you prefer players with “high expected points and high ownership”.
When you “maximize the net benefit” or “maximize expected points”, the optimization will pick the players higher on the diagonal (50% own direction). This will mean that you prefer players with “high expected points, regardless of ownership ratio”.
But, we can aim for something in between instead of these three extremes. Since we have two different objectives here, we can assign a weight on how much we think gain and loss are important.
$$ w \cdot \text{Expected Gain} - (1-w) \cdot \text{Expected Loss} $$
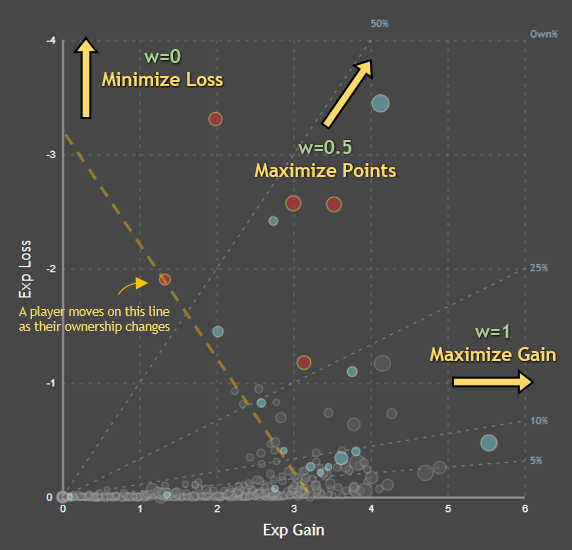
Notice that when $w=1$, you are maximizing your gain; when $w=0$ you are minimizing the loss, and when $w=0.5$, you are maximizing your points. Solving this problem using an optimization solver (algorithm) will give you what is called a “Pareto-optimal”. It means that, for the specified weight $w$, you will get the best solution. There could be other solutions that has the same value (weak Pareto optimality), but nothing can exceed this point on both objectives at the same time.
Yes, all FPL managers are trying to balance between their gains and losses, but there is an optimal selection of players for each selection of $w$ between 0 and 1. In case you are wondering how much this weight affects the optimal solution, I solved the resulting optimization problem (under 100M budget) for 21 different values of $w$. Here’s how the gain, loss and benefit changes for GW16:
| Gain Weight (w) | Exp Gain | Exp Loss | Exp Benefit (Net) |
|---|---|---|---|
| 0 | 28.850 | 27.736 | 1.114 |
| 0.05 | 28.850 | 27.736 | 1.114 |
| 0.1 | 30.576 | 27.896 | 2.680 |
| 0.15 | 30.576 | 27.896 | 2.680 |
| 0.2 | 33.740 | 28.664 | 5.076 |
| 0.25 | 35.172 | 29.138 | 6.034 |
| 0.3 | 35.172 | 29.138 | 6.034 |
| 0.35 | 36.801 | 29.951 | 6.850 |
| 0.4 | 36.801 | 29.951 | 6.850 |
| 0.45 | 39.216 | 31.686 | 7.530 |
| 0.5 | 40.885 | 33.090 | 7.795 |
| 0.55 | 43.116 | 35.548 | 7.568 |
| 0.6 | 43.116 | 35.548 | 7.568 |
| 0.65 | 45.277 | 39.203 | 6.074 |
| 0.7 | 46.487 | 41.486 | 5.001 |
| 0.75 | 46.487 | 41.486 | 5.001 |
| 0.8 | 47.376 | 44.378 | 2.998 |
| 0.85 | 47.376 | 44.378 | 2.998 |
| 0.9 | 47.376 | 44.378 | 2.998 |
| 0.95 | 47.376 | 44.378 | 2.998 |
| 1 | 47.376 | 44.378 | 2.998 |
The following chart might help to understand what is going on. You can hover (or touch) the circles below to see the actual lineup.
For GW17, the graph looks quite similar.
How to use this information?
That’s the million dollar question! As far as I can see, “Elite Managers” tends to minimize their losses. I assume if they need to select a $w$ value, it could be between 0.35 and 0.55, depending on how risk-averse they are. I was inspecting FPL Salah’s decisions for the last few weeks, and they are mostly on the conservative side. Check the expected and realized values for FPL Salah and Optimized FC (my team) for GW16:
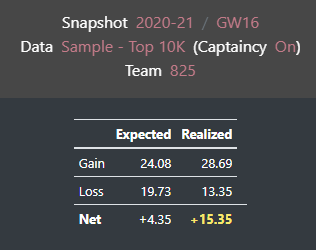
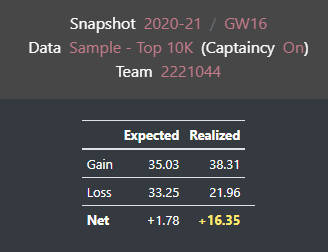
The expected net change is usually around these numbers, but FPL Salah’s expected gain and loss values are significantly lower. It indicates that my opponent goes for highly owned players more than I do.
Since it’s my first season in FPL, I’m not 100% sure what brings success in long-term, but I’m sure stable performance is quite important. Sudden jumps is not sustainable for obvious reasons. Another issue is that we only know the ownership rates for the current GW, so planning a few weeks in advance is tricky.
That’s why my optimization model focuses on total points for the planning horizon (8 gameweeks based on FPL Review data). I also keep an eye on ownership rates to see how much risk I’m taking. Since I’m committed to apply optimization model solutions as is, I expect a high Massive-Data (MD) value when using FPL Review’s “Season Review” tool. I suspect all the people who have high MD-points are using some sort of optimization in their decision making.
I created a page listing FPL managers who use analytics (and optimization) and sorted them by their MD points, rather than FPL points.
And if you are wondering how things look for your team for the upcoming (or past) gameweeks, visit FPL Optimized to see your expected gain and loss.
Conclusion
EO is a controversial issue and it will probably stay that way, but I think we demistified the role of EO in decision making. It’s not something FPL managers should be actively chasing, but an important component to adjust your expectations.
FPL is a multi-dimensional problem to solve, which I enjoy attacking using optimization models. Soon, I will share more on how a basic optimization formulation looks like for FPL. Meanwhile, you can see the source code on this Pareto-Analysis on my GitHub repository I keep for FPL Optimized.

